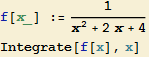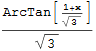3.4 Integrace racionálních lomených funkcí
Teorii naleznete v kapitole 6.4 Multimediální encyklopedie nebo v kapitole 3.4 Breviáře
Příklad 1
Vypočítejte
Řešení
U tohoto typu příkladu vystačíme se substituční metodou.
-5x+6 = t
-5dx = dt
dx = 
Odtud 
= 
. Tento integrál vypočteme pomocí programu Mathematica.
Na závěr dosadíme do výsledku substituci -5x+6 = t.
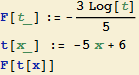
Při práci s programem Mathematica obvykle vypočteme příklad přímo:
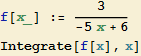
Příklad 2
Vypočítejte 
.
Řešení
Máme-li vypočíst integrál z podílu dvou polynomů, ve kterém je stupeň polynomu v čitateli větší nebo roven stupni polynomu ve jmenovateli, potom použijeme dělení polynomu polynomem. Pro dělení polynomu plynomem použijeme příkaz Apart, který rozloží zlomek na části s minimálním stupněm polynomu ve jmenovateli.
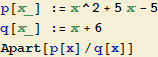
Můžeme tedy psát (za použití věty o linearitě integrálu):
=
= ∫-1+x dx + 
.
Integrál ∫-1+x dx vypočteme snadno.
Integrál 
je obdobný integrálu v Příkladu 1, vypočteme jej proto již přímo.
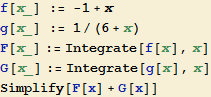
Při práci s programem Mathematica můžeme vypočítat integrál přímo:
Příklad 3
Vypočítejte 
.
Řešení
V tomto případě nelze použít dělení polynomu polynomem, protože stupeň polynomu v čitateli je nižší než stupeň polynomu ve jmenovateli. Při výpočtu na papíře se provádí rozklad zlomku na parciální zlomky. V programu Mathematica použijeme pro rozklad na parciální zlomky opět příkaz Apart.
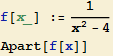
Nyní můžeme psát: 
= 
= 
-
. Výpočet zadaného interálu jsme převedli na výpočet dvou jednodušších integrálů, které se počítají substituční metodou obdobně jako v Příkladu 1.
Při práci s programem Mathematica ovšem dáme zpravidla přednost přímému výpočtu:
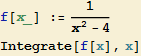
Příklad 4
Vypočítejte 
.
Řešení
Integrál vypadá zdánlivě velmi podoný jako v Příkladu 3. Ve skutečnosti ale diskriminant kvadratického trojčlenu ve jmenovateli je záporný a zlomek tak nejde rozložit na parciální zlomky. Proto nelze použít příkaz Apart.
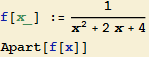
Řešením bude doplnění kvadratického členu ve jmenovateli na úplný čtverec.
= 
= 
=
= 
.
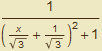Zvolíme substituci
= t
= dt
dx = 
dt
Nyní můžeme psát:
= 
= 
= 
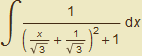. Tento integrál bychom měli znát zpaměti, můžeme jej ale i vypočítat programem Mathematica:
Ještě zbývá zpětné dosazení substituce:
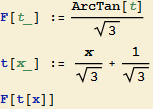
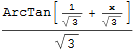
Při práci s programem Mathematica ovšem není nutno napodobovat postup, který bychom použili při výpočtu integrálu pomocí tužky a papíru. Integrál můžeme zadat přímo a Mathematica provede veškeré úpravy za nás.
